модель маркова
Состояния модели Маркова в графиках
- 06 августа 2016, 09:33
- |
Еще одна статья с ресурса www.talaikis.com по разработке простой стратегии на модели Маркова с использованием Python.
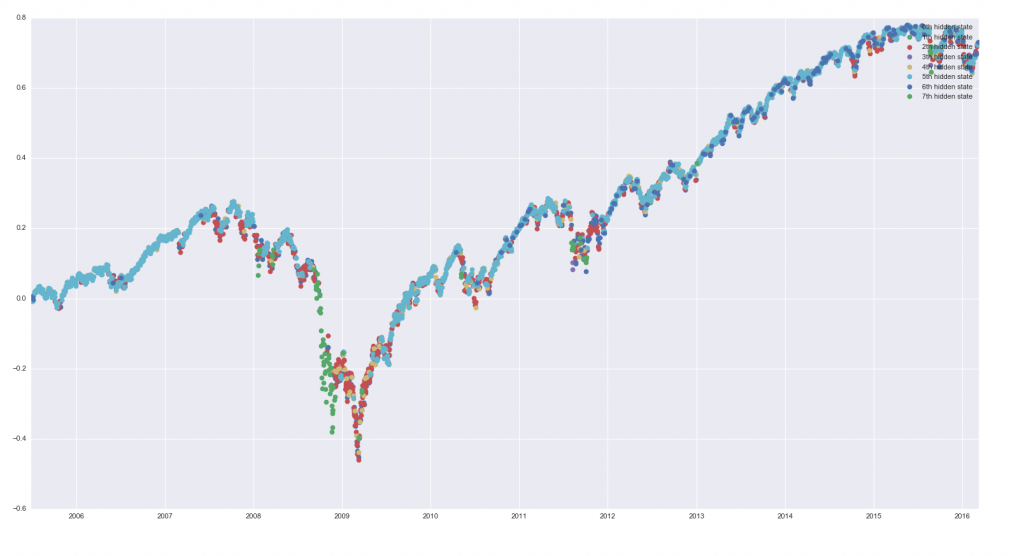
Модель скрытых состояний Маркова — это производительная, вероятностная модель, в которой последовательность наблюдаемых переменных генерируется некоторыми неизвестными (скрытыми) состояниями. Мы попытаемся найти такие неизвестные вероятностные функции для, скажем, S&P500. Все опишем кратко, без проверок на ошибки, без тестов вне выборки и т.д. Мы делаем это для того, чтобы минимизировать склонность к ненужному усложнению для начинающих. (Подробнее о модели Маркова см. на моем сайте — www.quantalgos.ru)
Что будем использовать:
библиотеку Python - hmmlearn.
1. Данные. Возьмем данные по свечам (OHLC), включающие объем, из нашей базы
( Читать дальше )
- комментировать
- 1.2К | ★19
- Комментарии ( 20 )
Тестирование модели Маркова на SPY
- 20 декабря 2015, 14:07
- |
По просьбе одного из читателей блога прогнал тесты инструмента SPY в моей программе, использующей модель Маркова для предсказания направления рынка. SPY- это биржевой символ фонда, повторяющего движения индекса S&P500, торгуется на бирже NYSE. Тестирование производилось на периоде от 01 июня 2015 года до 25 ноября 2015 года. Размер тренировочной выборки — 70%, выборки out-of-sample — 30%. Вот что получилось в итоге, для различных интервалов дискретизации:
1. 60- минутные бары:
( Читать дальше )
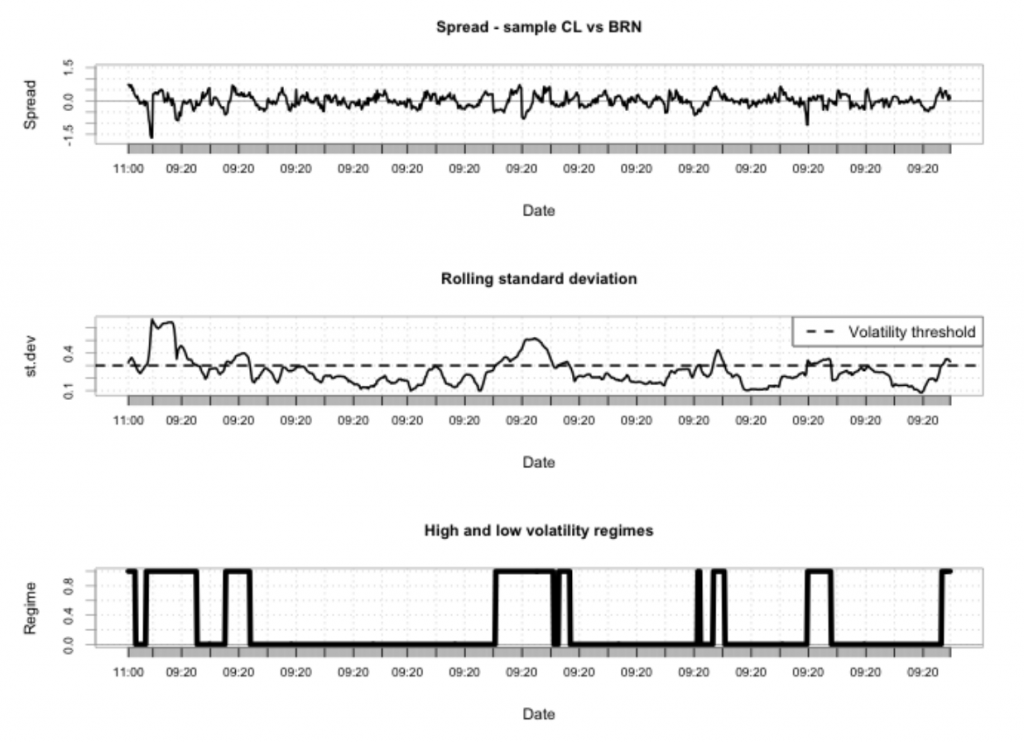
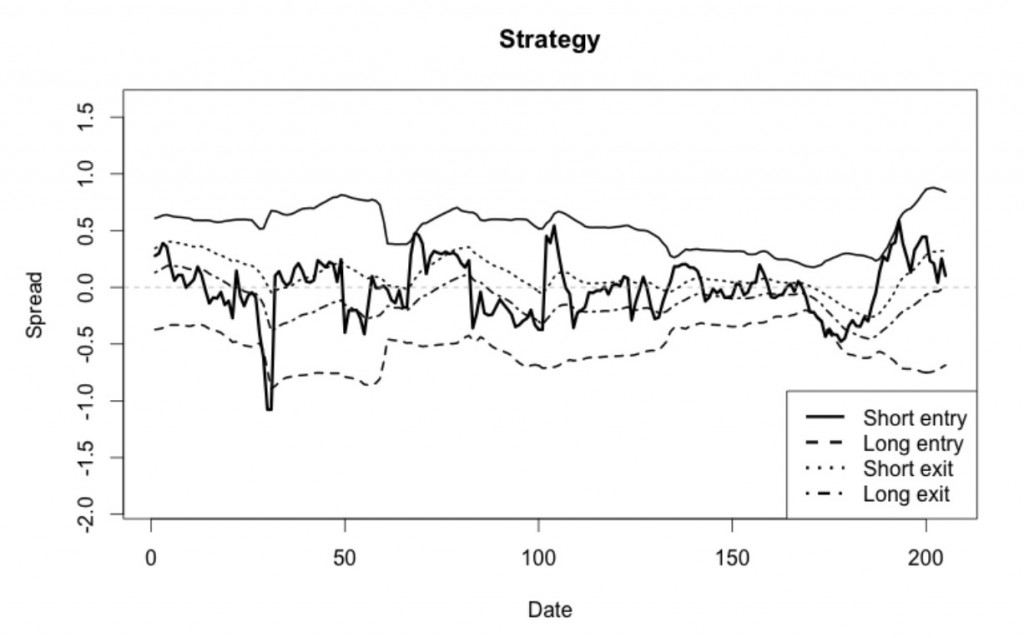
Парный трейдинг с переключением режимов. Часть 3
- 07 октября 2015, 09:03
- |
Окончание. Начало здесь.
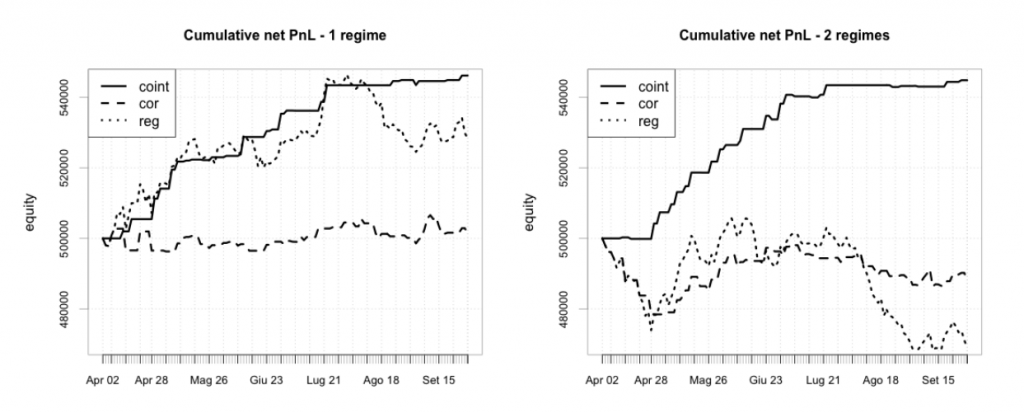
В соответствии со смоделированным спредом, мы предполагаем покупать (продавать) пять контрактов по одному активу, одновременно продавая (покупая) количество, равное [β×5], где [x] — целая часть х, по другому активу, так как число контрактов должно быть целым.
Мы моделируем торговлю с 500 000$ и наше гарантийное обеспечение будет примерно равным 20%. Мы не используем какую-либо технику манименеджмента, ГО 20% будет только в начале периода бэктестинга и будет снижаться по мере получения прибыли.
Итоговые результаты анализируются с помощью распространенных индикаторов, применяемых на практике: годовой коэффициент Шарпа, годовая доходность, максимальная просадка, доли дней с положительной и отрицательной доходностью, доля дней без сделок, коэффициент отношения среднего значения (в долларах) дней с положительной доходностью к дням с отрицательной доходностью, корреляция портфеля с индексом S&P500. Во всех случаях мы указываем чистый результат, принимая во внимание 3$ комиссии и один тик проскальзывания на сделку.
( Читать дальше )
Парный трейдинг с переключением режимов. Часть 2
- 29 сентября 2015, 08:58
- |
Продолжение. Начало здесь.
Модель, устойчивая к смене режимов волатильности
Некоторые проблемы торговли спредом
Ранее мы определили три сосотавляющих рыночно-нейтральных стратегий. Здесь мы обновим эту классификацию и рассмотрим некоторые трудности, связвнные с торговлей спредом.
Долговременные расхождения в ценах трудно найти с помощью алгоритмов, основанных только на ценах. Обычно, фундаментальный анализ, совместно с опытом трейдера может помочь в понимании существования расхождения. Время возврата к среднему может быть установлено с помощью непрерывных моделей, в этом случае период удержания позиции зависит от модели спреда и, следовательно, от частоты пересчета коэффициента хэджирования.
Много факторов могут приводить к скачкам волатильности спреда, но сами по себе скачки не могут быть приняты в качестве сигналов прекращения торговли парой.
( Читать дальше )
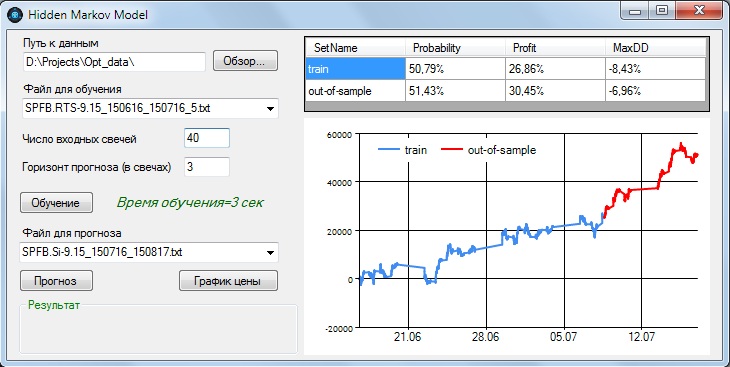
Проверка эффективности модели Маркова на фьючерсах FORTS
- 22 сентября 2015, 08:58
- |
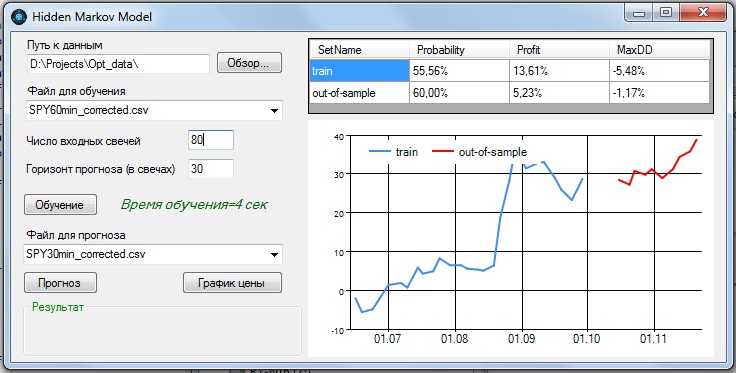
Ранее на моем сайте была опубликована статья по марковским моделям скрытых состояний (НММ) — часть 1, часть2, часть 3, часть 4. Мною разработана программа на основе этой публикации, с помощью которой была протестирована предсказательная способность HMM на некоторых инструментах рынка FORTS. Программа написана на языке C#, с применением сторонней библиотеки Accord.NET.
На вход программы подаются ценовые ряды фючерсов, представляющие собой последовательность свечей со значениями Open, Close, High, Low. Количество входных свечей можем задавать произвольно, эта величина является первым параметром. На выходе получаем прогноз на будущее направление движения цены. Горизонт прогноза в виде интервала, также измеряемого в количестве свечей, является вторым параметром. Третий параметр — это временной интервал самой свечи, определяется входным файлом. Исходные данные я брал с сайта Финам в виде текстовых файлов для каждого инструмента.
( Читать дальше )
Парный трейдинг с переключением режимов. Часть 1
- 16 сентября 2015, 09:04
- |
По итогам последнего голосования на моем сайте победила статья Marco Bee University of Trento — Department of Economics and Management,Giulio Gatti ,Università degli Studi di Trento — Department of Economics and Management — An Improved Pairs Trading Strategy Based on Switching Regime Volatility (Улучшенная стратегия парного трейдинга, основанная на переключении режимов волатильности). Ниже привожу перевод ее основных глав.
Введение
Стратегия, основанная на рыночно-нейтральном подходе, подразумевает, что трейдер должен принять три основные решения:
- Выбрать активы для торговли из набора множества торгуемых инструментов
- При существующем спреде ( т.е. динамически взвешенной разнице между двумя активами) определить его смысл в соответствующих эконометрических терминах
- Выбрать торговый алгоритм
( Читать дальше )
Пример использования VPIN и модели Маркова в торговле
- 14 августа 2015, 08:56
- |
Насколько успешным может быть применение индикатора токсичности потока ордеров VPIN в трейдинге? А если попробовать соединить его с моделью скрытых состояний Маркова? Пример такой стратегии приводит Dr Jonathan Kinlay в своем блоге. Напоминаю, что всю теорию по расчету VPIN вы сможете найти на моем сайте здесь, а по модели Маркова — здесь.
Для наших целей интерес представляет однопериодный знаковый VPIN. Он принимает значения от -1 до 1, в зависимости от пропорции между покупками и продажами за один период t — см. график в заглавии статьи.
Мы предполагаем, что приращение цены актива имеет сильную зависимость от значения VPIN. Например, в тестах фьючерса ES, мы увидели, что изменение средней цены от одного объемного пакета ( см. теорию VPIN) до следующего высококоррелировано со значением VPIN в предыдущем пакете с коэффициентом 0,5. Другими словами, участники рынка, предоставляющие ликвидность, будут обновлять свои ордера в направлении, которое прямо связано с направлением и интенсивностью потока токсичности.
( Читать дальше )
Модель скрытых состояний Маркова. Часть 4
- 20 мая 2015, 14:06
- |
Окончание цикла статей. Начало и другие алгоритмы биржевой торговли смотрите в моем блоге и на сайте.
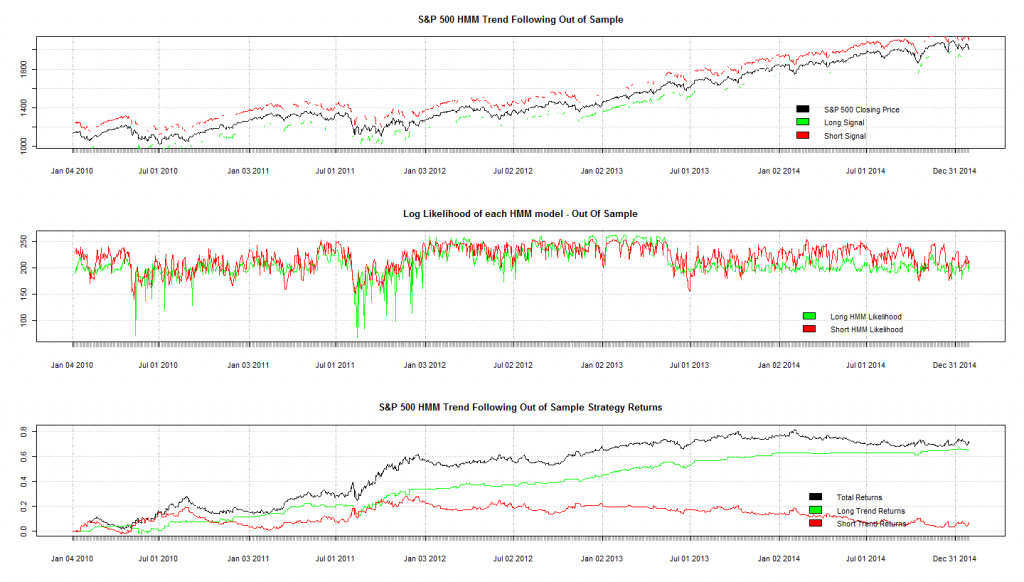
В прошлой части мы продемонстрировали обучение модели Маркова на данных, полученных с помощью симуляции. В данной статье рассмотрим производительность модели на реальных данных. Будем тестировать трендследящую стратегию на индексе S&P500.
В большинстве задач с использованием машинного обучения требуются обучающие данные с разметкой классов (состояний). В нашем случае такой разметки нет, поэтому сначала сгенерируем классы для обучающей выборки.
Мы хотим создать трендследящую стратегию, поэтому должны выбрать участки на выборке цен S&P500, которые соответствуют восходящему и нисходящему трендам ( также можно отметить участки, где тренды отсутствуют). Можно это сделать вручную, а можно применить программу, которая автоматически расставит метки в соответствии с вашими определениями тренда.
( Читать дальше )
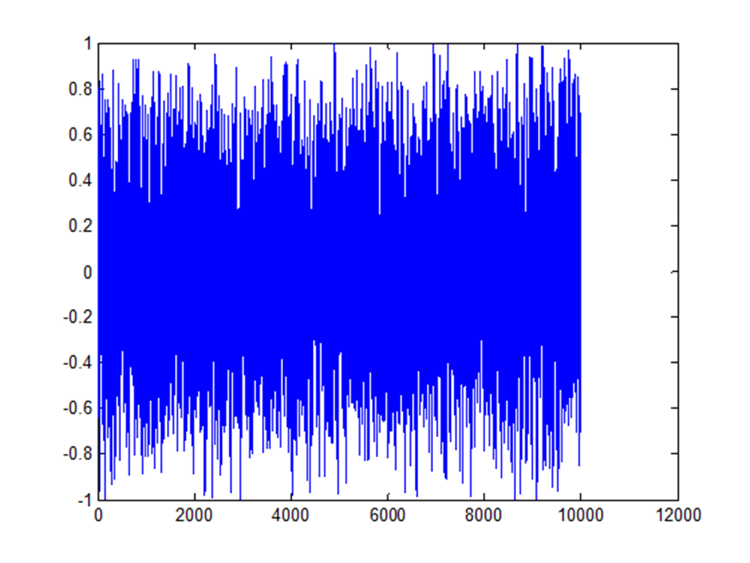
Модель скрытых состояний Маркова. Часть 3
- 18 мая 2015, 14:01
- |
В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
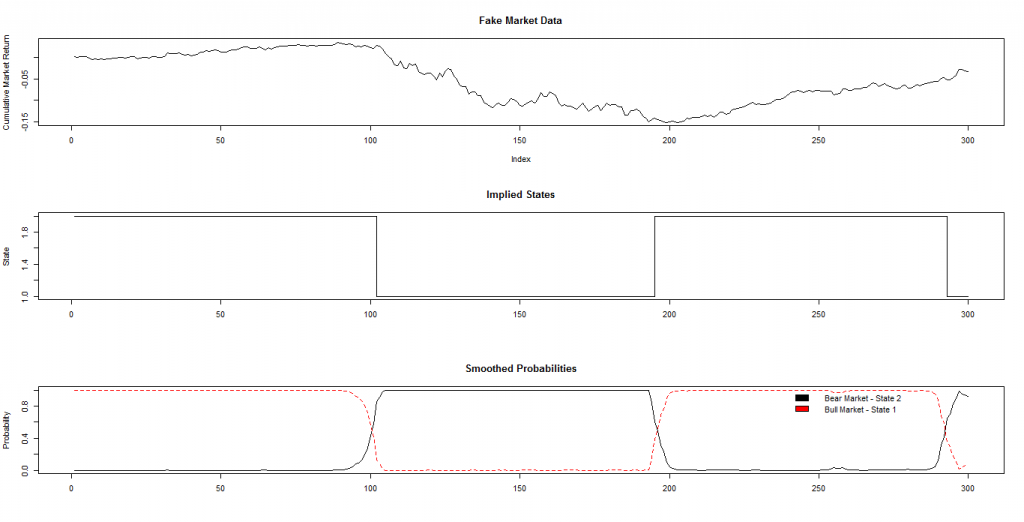
Метод первый — одна модель с несколькими состояниями.
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
( Читать дальше )
Модель скрытых состояний Маркова. Часть 2
- 14 мая 2015, 13:34
- |
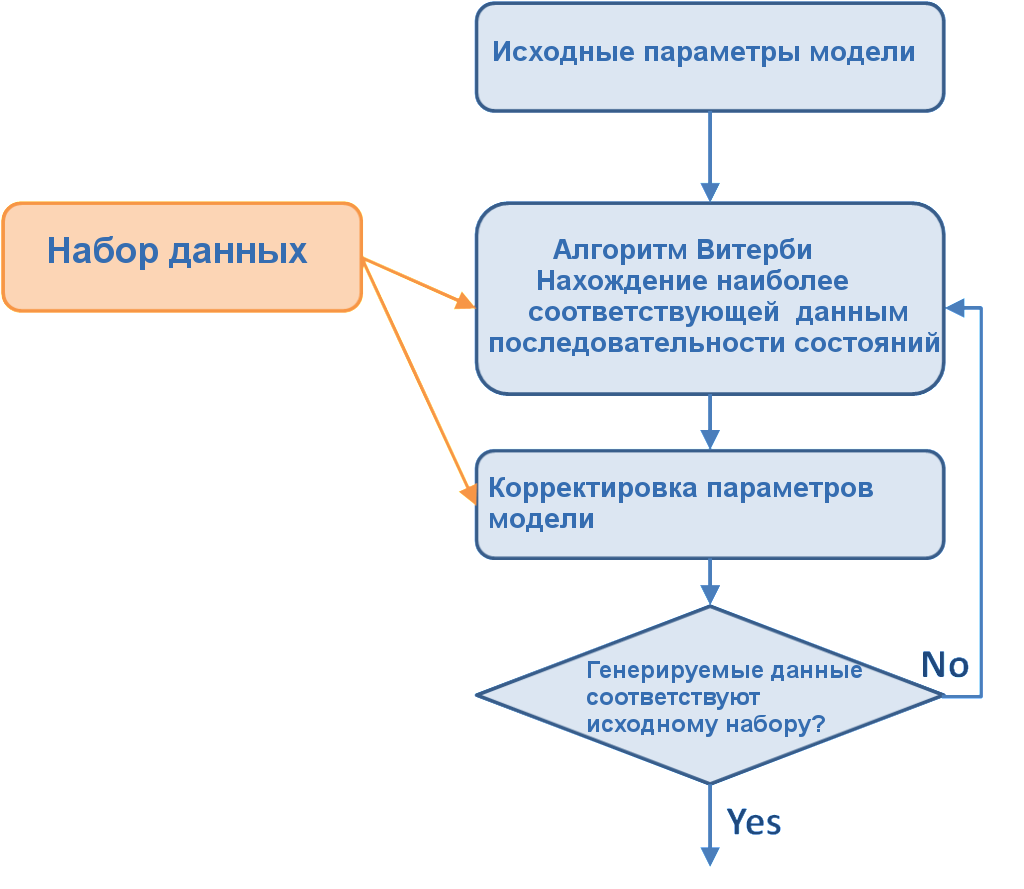
В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность соответствия данных наблюдения полученным моделью всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность соответствия данных полученной моделью одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности p(O|λ). Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал